(WIP) Introduction to Control Theory
This post is a summary of the paper titled Introduction to Control Theory And Its Application to Computing Systems.
What is control theory
Control theory is a way of desiging feedback in systems so that
- the signal doesn’t oscillate too much
- the signal is accurate in achieving objectives such as response times
- the signal settles to a steady value
As you can imagine, this becomes quite useful in monitoring complex systems. The usage of control theory does go beyond metrics though. Flow control depends heavily on real-time information to make decisions. An example would be throttling TCP/IP packets over a network.
The controller component
One of the key ideas behind control theory is the idea of having a component in a system called a controller. The controller is then able to adjust parameters of poorly performing components to create a well performing system.
In order for the controller to be able to do what it’s desingned to do, it must have access to the input signals of the system, the rate of error, and the controlls of the system (among other parameters). Once those parameters are available, the controller should be able to predict and account for oscillations in signal.
A diagram was presented in the paper along with a more detailed explanation of how these parameters work.
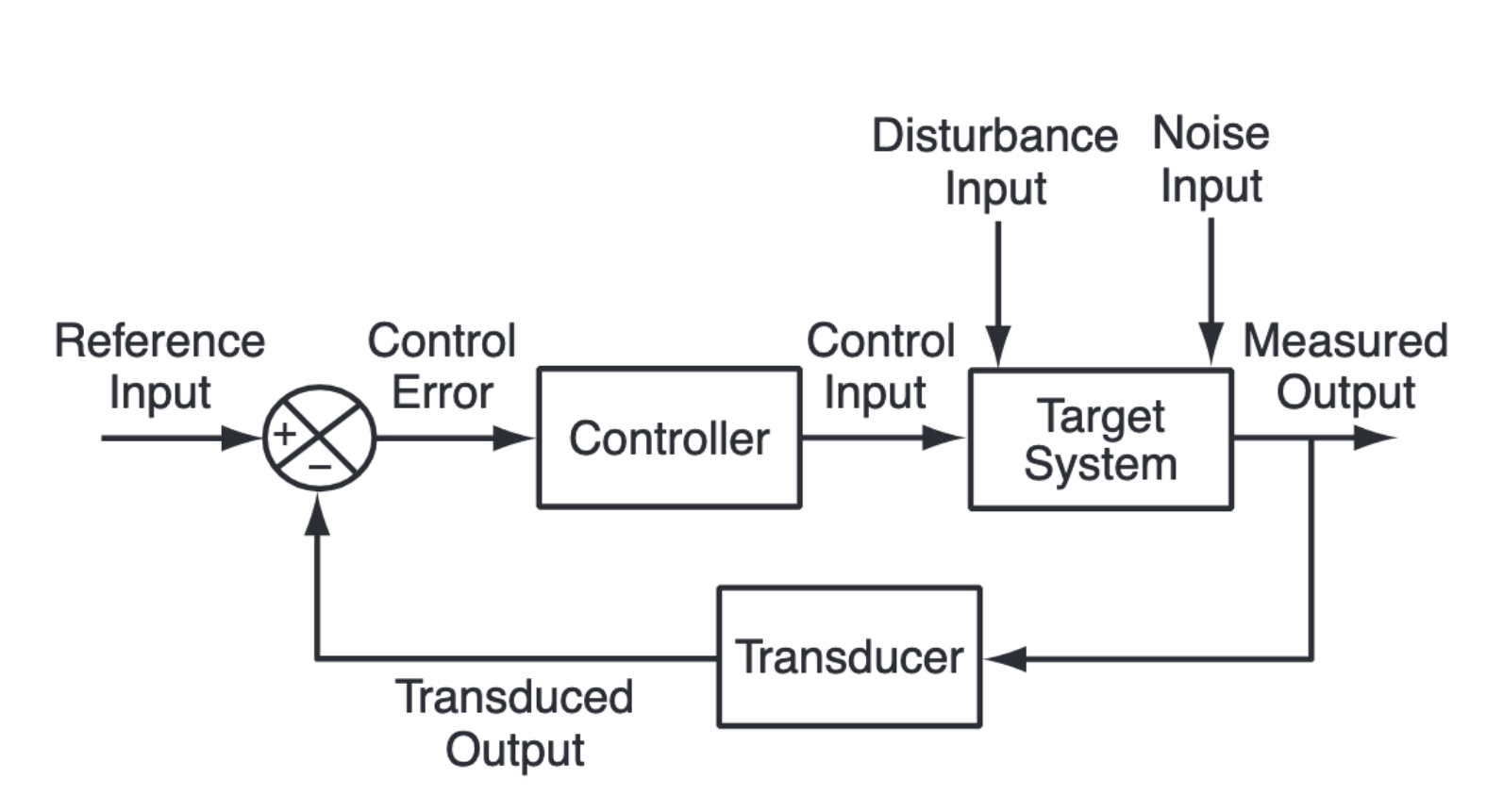
Most common usages of a controller are
- Regulatory Control, where there is a desired goal (say all computers at 70% capacity) and the controller tries to balance the value in relation to said reference input.
- Disturbance Rejection, where the controller tries to circumvent unplanned disturbance (disturbance input) while maintaining some level of service (for example maintaining 70% capacity in light of unplanned virus scans).
- Optimisation, where you adjust parameters to get the best output (example adjusting number of connections to get the lowest latency times). There is no reference input here.
Example of properties used for measuring systems
The subject paper relies heavily on their example of monitoring IBM DB2 (database) and Lotus Domino Server (office tools such as calendar). Because of that, the example relies on the following properties to be considered
- Stability, where for bounded input the output is also bounded.
- Accuracy, where given some input, the output converges to the desired value. This is usually measured as inaccuracy.
- Short settling times, where the outputs are quick to converge.
- Overshoot, or rather lack of overshooting. This occurs when drastic changes are made to achieve goals. This is unfavourable since overshoot tends to lead to undershoot.
The papers Lotus Domino Server example is called an LTI, a linear time-invariant deterministic system. Such a system is characterised by having 1 input and 1 output and is a closed circuit (like in the diagram above). There are many extensions to the LTI theory such as Adaptive Control, Stochastic Control, and others.